- Sarah Sword
- Senior Research Scientist
- Assessing Secondary Teachers' Algebraic Habits of mind
- http://mhomresearch.edc.org
- Education Development Center
- Courtney Arthur
- Assessing Secondary Teachers' Algebraic Habits of mind
- http://mhomresearch.edc.org
- Education Development Center
- Al Cuoco
- Distinguished Scholar
- Assessing Secondary Teachers' Algebraic Habits of mind
- http://mhomresearch.edc.org
- Education Development Center
- Miriam Gates
- Researcher
- Assessing Secondary Teachers' Algebraic Habits of mind
- http://mhomresearch.edc.org
- Education Development Center
- Ryota Matsuura
- Associate Professor of Mathematics
- Assessing Secondary Teachers' Algebraic Habits of mind
- http://mhomresearch.edc.org
- St. Olaf College
- Glenn Stevens
- http://math.bu.edu/people/ghs/index.html
- Professor of Mathematics
- Assessing Secondary Teachers' Algebraic Habits of mind
- http://mhomresearch.edc.org
- Boston University
Public Discussion
Continue the discussion of this presentation on the Multiplex. Go to Multiplex










Andrew Izsak
Have you found that some practices are more difficult to support than others? In our work in content courses for future middle and secondary teachers, we have noticed that some begin to reason from definitions more quickly than others. This fits under SMP3. Have you also noticed that teachers have trouble developing this practice?
Miriam Gates
Sarah Sword
Glenn Stevens
Professor of Mathematics
Miriam Gates
Sarah Sword
Rob Wieman
Are there particular pedagogical moves that teachers seem to take up, that are connected to particular habits of mind? Are you able to disentangle the effect of their mathematical knowledge from their experience of instruction in terms of their take-up of specific pedagogical practices (i.e. how do you know that they are more likely to teach in a particular way because of their newfound mathematical habit of mind or because they were taught that way in the project?) Is it possible to teach to particular habit of mind if I am still working to cultivate it in myself?
Miriam Gates
Sarah Sword
Sarah Sword
Senior Research Scientist
Hi Rob - the last question feels like the easiest: in general, I don't think any of thinks a habit is ever "cooked" - you get better and better at identifying and using (for example) mathematical structure over the course of your mathematical life, even if you're doing mathematics research. So in some sense, everyone is always working to cultivate habits in themselves. My suspicion is that it's possible to teach a habit of mind if you find that habit interesting, relevant, and useful. Having said that, we see teachers who do have strong habits - and who also believe that students can develop those habits - doing fairly amazing things with their students in terms of fostering habits in their students.
As for pedagogical moves - I'm not sure what counts as a move, but we do see certain approaches associated with mathematical habits - teachers who offer students concrete experiences before moving to general or abstract definitions or ideas, letting students in on development of ideas and not just finished mathematical products, and modeling clear use of mathematical language.
As for disentangling mathematical knowledge, experience, and other factors... you know how hard that is. We've been immersed in studying the habits and practices of teachers in one very large high school - the teachers work closely together, they share a lot of common practices, and they've shared a lot of common habits-of-mind-based PD. It would be impossible for any one program to "take credit" for the practices that we see in those teachers. But they have had coherent PD experiences as a department, they work closely together, they constantly learn from each other, and it shows.
Miriam Gates
Al Cuoco
Distinguished Scholar
Hi Rob,
Like Sarah, I'm not sure what counts as a pedagogical move, but I have seen teachers with whom we work shift focus and emphasis away from simply using results towards a more balanced treatment between using and establishing.
For example, in algebra classes some teachers (not all) are hammering at the habit of abstracting regularity from numerical examples in order to build equations and functions that model situations. Students practice [sic] this practice in everything from setting up equations to model word problems to finding Cartesian equations for geometric objects, and these folks explicitly call out this habit when it comes up in student work.
I think I know the school to which School Sarah refers, and I can vouch for the fact that the incoming mathematical backgrounds and dispositions are all over the place. They have the luxury of getting together once a month to work on problems, and, yes, some are much more facile with mathematical thinking than others. But they all appreciate the approach of experience before formality (because, well, they experience it) and cite reasons that range from ``the kids get it'' to ``it saves time in class'' to ``fewer methods to learn.''
Al
Miriam Gates
Sarah Sword
Heidi Larson
Project Director
Thanks for your video -- very interesting! I hope it will help to recruit teachers for your field testing.
How are schools using this assessment with their teachers? Once they have administered it, what happens then?
Sarah Sword
Sarah Sword
Senior Research Scientist
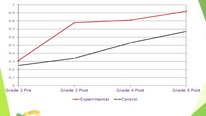
Hi Heidi, thank you for your questions. There are two main ways programs have used the assessment: one is diagnostically - determining where groups of teachers could use more support in developing mathematical habits of mind. The other way we've seen it used is as a pre- post- measure of PD programs success in fostering mathematical habits of mind. In each case, we can provide summaries of groups of teachers' scores across each of three dimensions: language, seeking structure, and using structure.
Heidi Larson
Miriam Gates
Miriam Gates
Researcher
It is also notable that in cases where the instrument has been used diagnostically, it can also lead to some really rich discussions among teachers in a district or school. As highlighted in the video, the tasks are designed to lend themselves to multiple approaches. We have heard from teachers that using the instrument as a vehicle for discussion can be instructive, provide opportunities to discuss the different approaches with colleagues, and be fodder for interesting classroom practice discussions.
Heidi Larson
Sarah Sword
Jennifer Yurof
Thanks for sharing your project - very interesting work! Do you offer resources for teachers to alter their habits of mind?
Sarah Sword
Miriam Gates
Researcher
Hi Jennifer, Thanks for the question.
While our project was designed to measure the impact of programs that would seek to impact these habits, there are a number of programs that do target these habits. In the realm of in person professional development opportunities, two intensive summer mathematics experiences would be Promys for Teachers (a piece of which is shown in the video) and PCMI’s Teacher Program.
In terms of written resources that focus on these ideas, the PCMI materials have recently been published with facilitator notes, solution sets, and discussions of how the ideas fit into the mathematical landscape. The Developing Mathematical Ideas series also focuses on the big ideas of mathematics at K-8 and can serve to support teachers in developing mathematical ideas and think about their application to the classroom.
Heidi Larson
Steven Rogg, Ph.D.
Sarah Sword
Steven Rogg
Associate Professor of Education - STEM
With the diagnostic and PD applicaitons that you cited, I'm curious if anyone has coupled the assessment with Lesson Study in mathematics? The focus of lesson study being on student response in a lesson, it would add a dimension of understanding, I think, to also have a companion tool for teacher habits of mind. Perhaps?
Sarah Sword
Senior Research Scientist
This is really interesting, Steve, because all of our work on the assessment has come from one kind of "teacher response" or another - most of the items were taken from interesting things we saw in teachers' classrooms, and all of the rubrics were built from teacher responses and interview data that we collected early in the project. But also: one of the most fun things we've done in the project is debrief with teachers after they've taken the assessment - it's fun to talk about habits of mind/Standards for Mathematical Practice, and how teachers see those standards and habits represented in the assessment items.
Do you have a sense of what such a tool would look like?
Thanks for your comment and question!
Steven Rogg, Ph.D.
Steven Rogg
Associate Professor of Education - STEM
Thanks, for your reply, Sarah. I am intrigued by the emergent design from teacher response which then cycles back as feedback when debriefing the assessment. To answer your question, I'd serve you better to refer you to my good colleagues Tom McDougal and Akihiko Takahashi at info@LSAlliance.org. I look forward to watching your work inspire algebraic habits of mind!
Further posting is closed as the showcase has ended.